Merkle trees: a visual introduction

Posted by Sacha Saint-Leger on January 30, 2020

Merkle trees are a fundamental part of what makes blockchains tick… Thanks to Merkle trees, it is possible to build Ethereum nodes that run on all computers and laptops large and small, smart phones, and even internet of things devices…
–Vitalik Buterin

In this visual essay, we try our best to explain Merkle trees from first principles. The only assumption we make is that you have a basic understanding of what blockchains are, and that you’re familiar with the concept of a binary tree.

If you’ve been in the blockchain space for a while, you’ve likely come across Merkle trees before: the Bitcoin blockchain uses them to store the transactions in every block, while Ethereum contains not just one Merkle tree, but three trees.

While we won’t get into the details here, every block header in Ethereum contains three trees, for three kinds of objects: to handle transactions, receipts (pieces of data showing the effect of each transaction), and state. If you want to find out more, see this excellent post by Vitalik.

Why do we care? At Iden3, one of our major goals is scalability. Specifically, we believe anybody should be able to create as many identities as they want. And that any identity should be able to generate as many claims as they want.

Merkle trees are one of the keys to achieving this goal (we’ll dig deeper into the why’s and how’s in a follow-up post).

But before we get to Merkle trees, it’s important to first understand what a hash function is. Hash functions are a key part of the Merkle tree operating system.

Hash functions

A hash function basically maps an input string of any size to an output string of a fixed size.

It must be efficiently computable – by that we mean that for any given input string, we can figure out the output of the hash function in a reasonable amount of time. More technically, computing the hash of an n‐bit string should take O(n) time.

For a hash function to be cryptographically secure, it must have three additional properties:

Collision resistance
Hiding
Puzzle-friendliness

While we won’t get into the details here, let’s briefly discuss what each of these properties mean.

Collision resistance means that nobody can find two inputs that map to the same output.

Hiding means that given an output there’s no feasible way to figure out the input that generated it. In other words, the hash function is irreversible.

Puzzle-friendliness is a little more complicated. Intuitively it means it’s very hard to target the hash function to come out to some particular output value y. Don’t worry if you don’t see why this property is useful, for the purposes of this article, it isn’t very important.

To be slightly more formal: Take: y = H(x|r). Where y is the output of the hash function H, and r and x are the inputs.

The hiding property specifies that given an output ( y ), it is infeasible to find an input ( x ) such that y = H(x|r) is satisfied. Note, that in this case r is not given (in other words, hidden).

Puzzle-friendliness means that given the output ( y ) and part of the input ( r ), it is difficult to find an x such that y = H(x|r).

If there’s one thing to take away from all this, it’s that hash functions allow us to store a cryptographic hash of a data value at some fixed point in time.

If at some point in the future, we want to check the data hasn’t changed, we simply hash the data again and check that the new output (cryptographic hash) matches the previous output.

This works because we know by the collision resistance property of the hash function, that nobody can find two inputs that map to the same output. So if the output is the same, the input must also have been the same.

Now that you have an intuitive understanding for what a hash function is, we’re ready to tackle Merkle trees :)

Merkle tree

The most common and simple form of Merkle tree is the binary Merkle tree. A binary Merkle tree is a binary tree built using hash functions (since this is the form we’ll be focusing on in this essay, we’ll omit the binary prefix from now on).

Merkle trees are useful when we want a data structure that:

Can store lots of data (scalability)
Makes it easy to prove that some data exists (proof of membership)
Allows us to check that data hasn’t been altered (tamper resistance)

As you can probably see, these properties make them a natural use case for blockchains.

Note: at Iden3 we use a slightly more complex data structure called a sparse Merkle tree. Sparse Merkle trees have an additional property: they make it easy to prove that some data doesn’t exist. But we’ll talk more about that in another post.

Specification

Before we take a closer look at proof of membership and tamper resistance, let’s go through how to build a Merkle tree given some data:

Suppose we have a number of blocks containing data. And that these blocks make up the leaves of our tree.

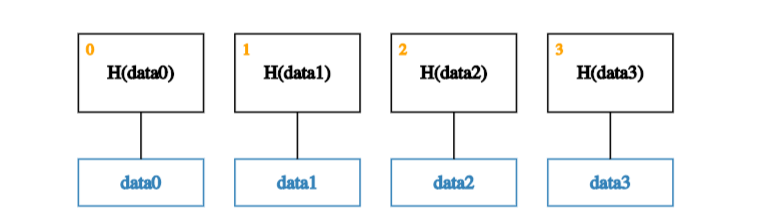
The first step is to create a parent node for each data block. These parent nodes make up the next level in the tree and store the hash of their descendent data block.

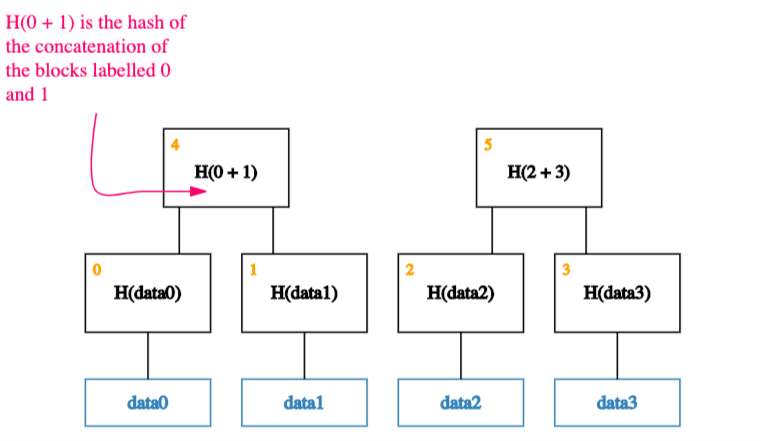
Next, we group the parent nodes into pairs, and store their hashes one level up the tree.

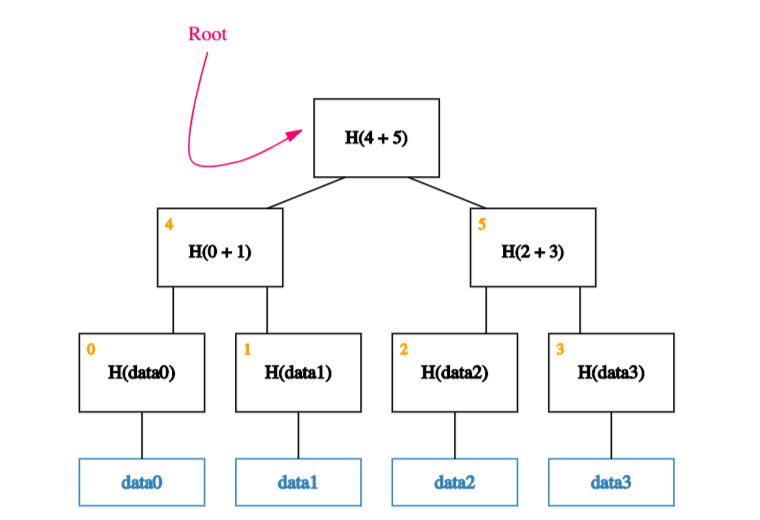
We continue doing this until we reach a single block, the root of the tree.

Tamper resistance

It turns out that any attempt to tamper with any piece of data can be detected by simply remembering the hash at the root of the tree.

To understand why this is the case, let’s look at what happens if an adversary wants to tamper with a data block:

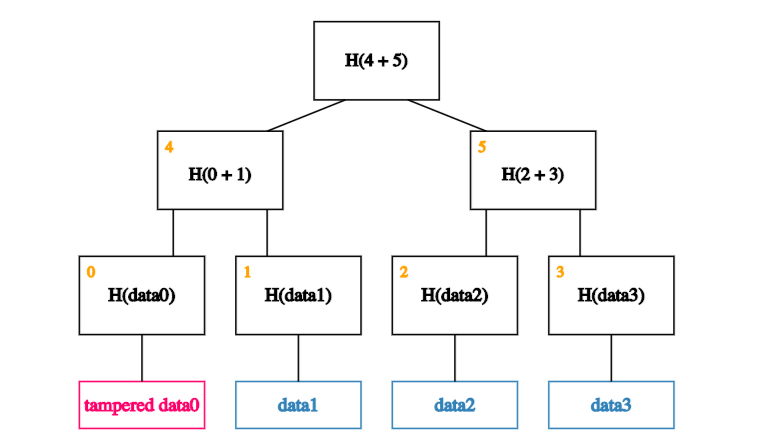
If an adversary tampers with a block at the leaf of our tree.

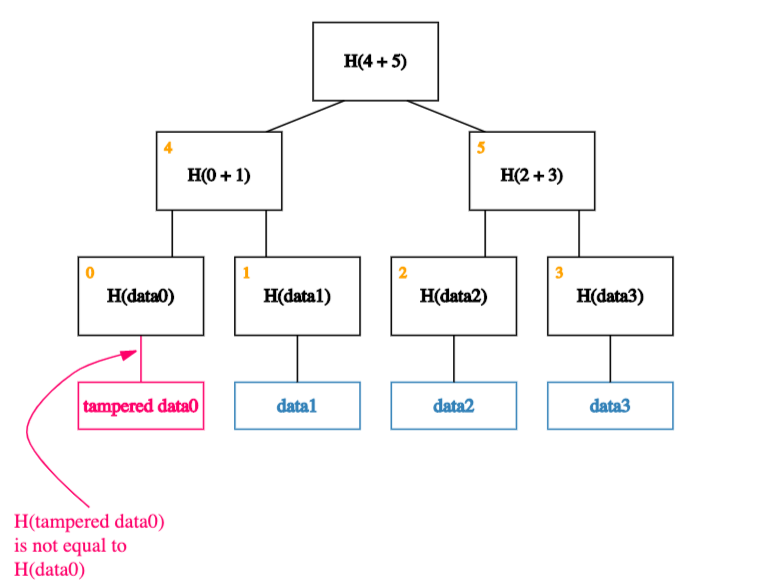
That will cause the hash in the node that’s one level up to not match.

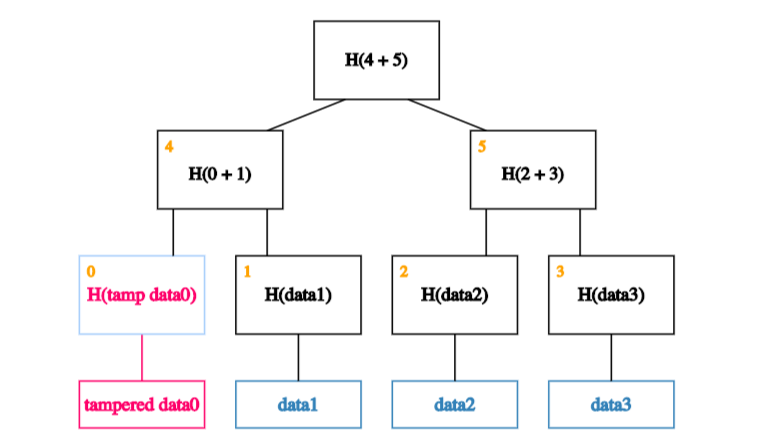
So he’ll have to tamper with that too.

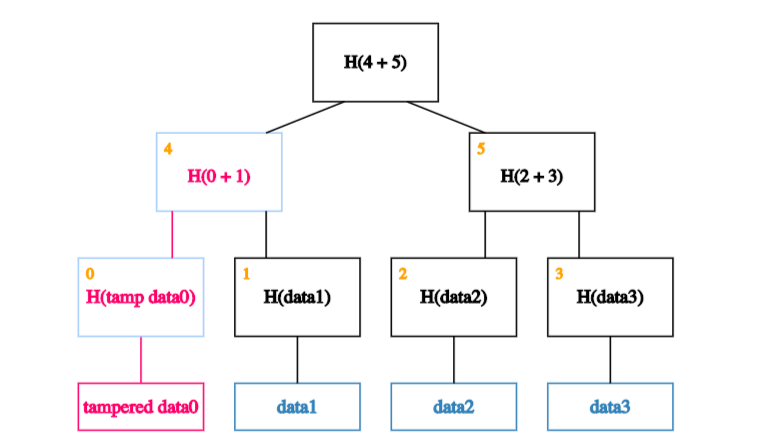
Which means, he’ll have to tamper with the node one level up from there.

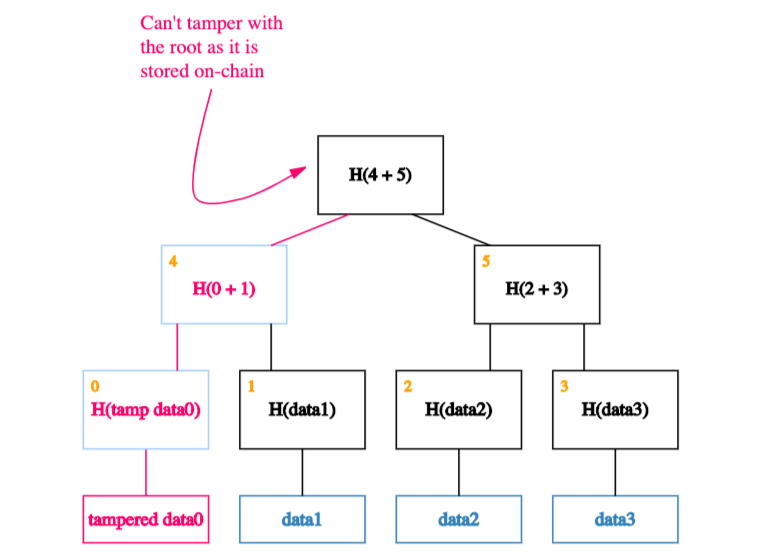
And so on… Eventually he’ll get to the root. If he tries to tamper with the root, we’ll know because this is the node we’ve kept track of.

Proof of membership

Merkle trees allow us to quickly check membership (through a neat mechanism known as Merkle proofs). What do we mean by that?

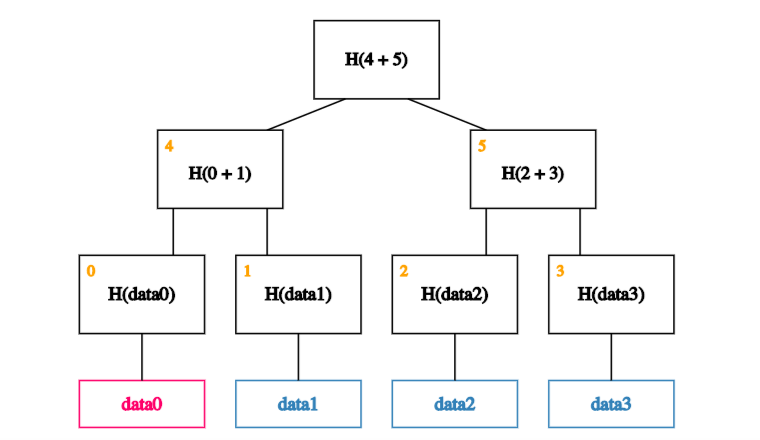
Say that, as usual, we remember just the root (on-chain). And we want to prove that a certain data block - data0, say - is a member of the Merkle tree.

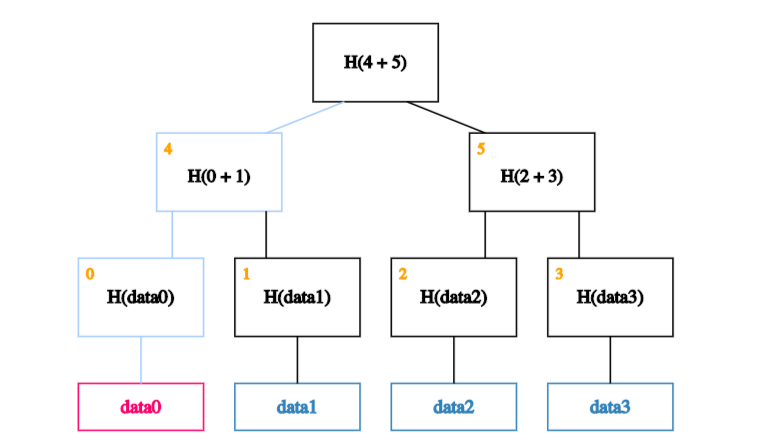
All we need are the blocks on the path from the data block to the root.

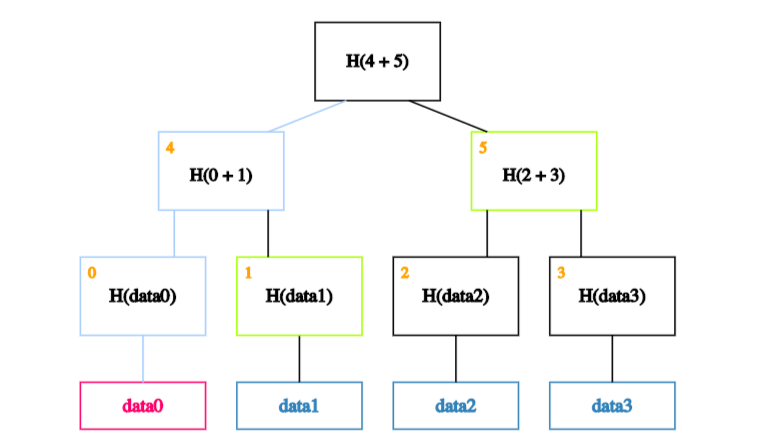
And each of data0’s siblings on the way up the path.

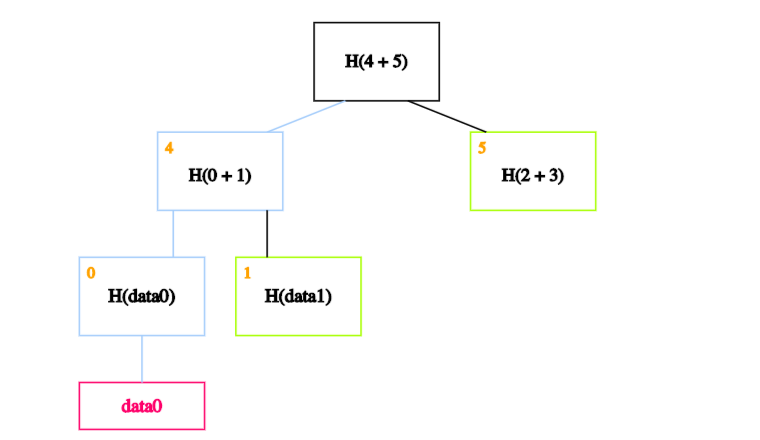
We can ignore the rest of the tree, as these blocks are enough to allow us to verify the hashes all the way up to the root of the tree. How exactly?

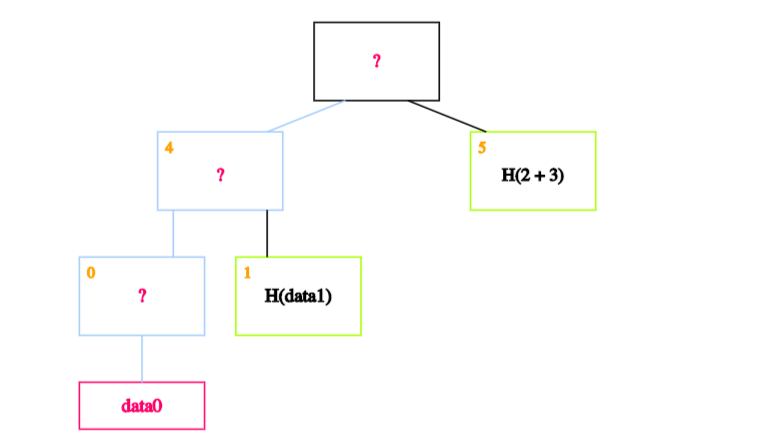
The idea is to recalculate the root by recursively hashing the data we want to prove exists. If the calculated root is equal to the on-chain root, this proves the data block exists in the Merkle tree.

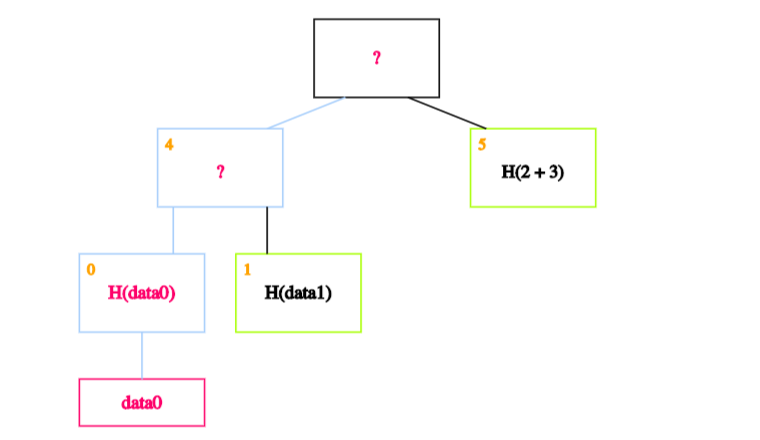
In our case, we start by calculating the hash of data0 and storing it in the block labelled 0.

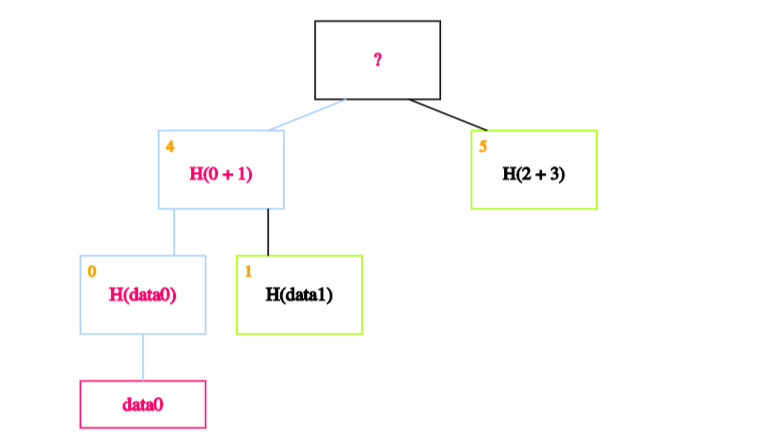
We then calculate the hash of the hash of data0 concatenated with the hash of data1 - in other words, the hash of the concatenation of blocks 0 and 1 - and store it in block 4.

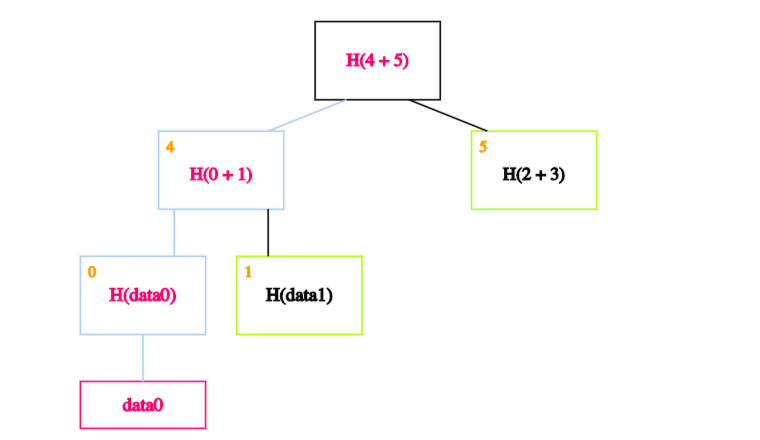
Finally, we calculate the hash of blocks 4 and 5 to obtain the recalculated root.

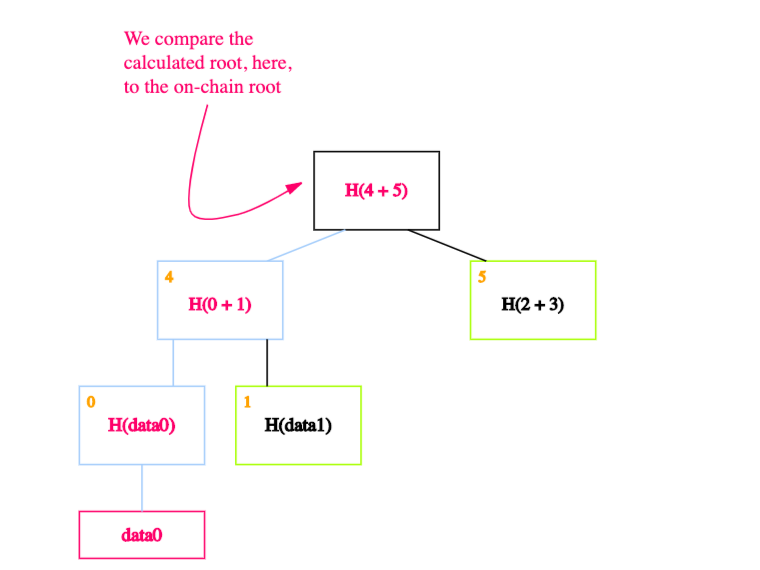
If the calculated root is equal to the on-chain root, we’ve proven that data0 exists in the Merkle tree.

In technical terms: This means that if there are n nodes in the tree, only about log(n) items need to be shown. And since each step just requires computing the hash of the child block, it takes about log(n) time for us to verify it. And so even if the Merkle tree contains a very large number of blocks, we can still prove membership in a relatively short time. Verification thus runs in time and space that’s logarithmic in the number of nodes in the tree. Source (pg 35)

Summary

In sum, Merkle trees are handy because they have some nice properties that help us minimize the amount of data we need to store on-chain. And this is important because storing data on a blockchain is expensive.

More specifically, to ensure tamper resistance and proof of membership we only need to keep track of the root of the tree.

In other words this means that, no matter how big the tree is, the only piece of data we need to store on-chain is the root.

We hope this you found this introduction useful. We’ll be digging deeper into how we use Merkle trees at Iden3 in a series of follow up posts.

In the meantime, if you’re curious to know more about Merkle trees and their applications in Ethereum, we recommend reading throught this excellent essay by Vitalik.

iden3.io