Nectar Token Airdrop : Under the hood 🤓

Posted by Sacha Saint-Leger on November 22, 2019

During this year’s Devcon, more than 400 people took part in our TrustCommunity experiment, interacting with each other and earning Nectar tokens. As of November 11 participants can withdraw their tokens from a smart contract without revealing their identities. Here’s how it works 🤓:

When a participant visits the TrustCommunity web app, they are prompted to retrieve a claim from the application server. For those of you who are unfamiliar with the concept of a claim, you can think of a claim as a statement. Most of the time, these statements refer to identities.

For example, when a university (identity) says that a student (identity) has a degree, this is a statement (claim) about the student. This statement creates a relation between the student and the university.

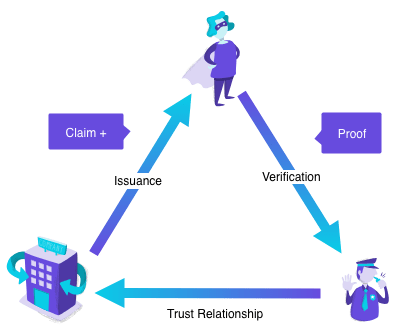
Claims can be public or private. And it turns out that almost anything we say or do can be thought of as a claim. Company invoices, Facebook likes, email messages, can all be thought of as claims.

In the TrustCommunity case, each claim contains the identity of the user and the amount of Nectar tokens the identity earned.

Each claim is stored as a leaf in a Merkle tree, with just the root of the tree (the Merkle root) published on the Ethereum blockchain. This root is all one needs to verify the integrity of the claims.

Importantly, the root does not reveal any information about the information stored in the leaves. In other words, the root does not reveal anything about the claims in question.

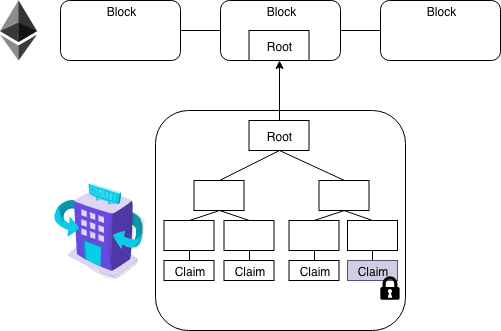
While we won’t get into the weeds here, you can think of a Merkle tree as a binary tree built using hash pointers.

Merkle trees are special because they:

1. Can store lots of data (scalability)
2. Make it easy to prove that some data exists (proof of membership)
3. Allow us to check that data hasn’t been altered (tamper resistance)

At iden3 one of our major goals is scalability. Specifically, we believe anybody should be able to create as many identities as they want. And that any identity should be able to generate as many claims as they want.

Imagine if you had to make a new transaction to the blockchain every time you wanted to make a new claim? Even worse, imagine you’re a government and you’re responsible for making millions of claims every day… It would simply be too expensive.

So to achieve this goal requires minimizing the amount of data stored on chain. This is where Merkle trees come in. A government making millions of claims a day, can construct a tree (off chain) with each claim as a separate data block, and simply calculate and store the root on chain.

In other words, Merkle trees allow prolific claim generators to add/modify millions of claims in a single transaction. This makes it financially feasible to scale claims.

Remember that a Merkle tree is just a binary tree built using hash pointers. And a hash pointer is simply a pointer to where some information is stored together with a cryptographic hash of the information.

Why use a hash pointer instead of a normal pointer? A pointer gives you a way to retrieve the information, whereas a hash pointer also gives you a way to verify that the information hasn’t changed.

In other words, a hash pointer is a pointer to where data is stored together with a cryptographic hash of the value of that data at some fixed point in time.

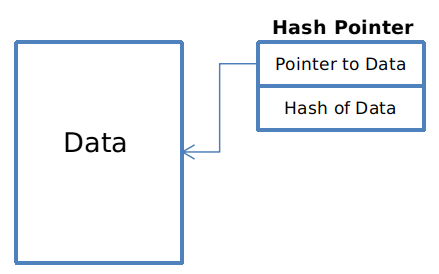
If at some point in the future, we want to check the data hasn’t changed, we simply hash the data again and check that the new output (cryptographic hash) matches the previous output.

This works because we know by the collision resistance property of the hash function, that nobody can find two inputs that map to the same output. So if the output is the same, the input must also have been the same.

There are many different types of hash functions, each with slightly different properties. In the TrustCommunity experiment we’re using the Poseidon Hash function.

Poseidon is a zk-SNARK friendly hash function. Which basically means that it’s cheap in certain (proofsystem-dependent) metrics. It’s this cheapness that allows proofs to be generated & verified in reasonable time.

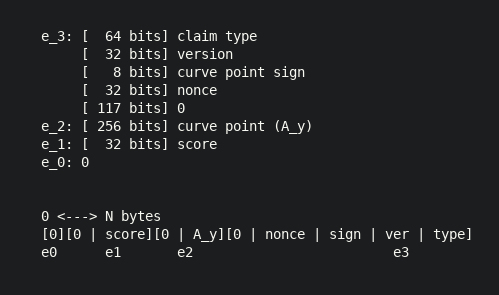
For the more technically inclined, under Poseidon, claims consist of four elements, each of which is a point of the large prime subgroup of the Baby Jubjub elliptic curve.

And while we won’t get into the gory details here, if you’re curious as to why Baby JubJub is optimal for zk-SNARK operations, see this excellent post.

In our case, there are two elements of importance: one of the elements represents the score (e_1) and another represents the public key of the associated identity (e_2).

As outlined in last week’s post, when a user — let’s call her Marta — wants to withdraw her Nectar tokens, she first loads the TrustCommunity web wallet, imports a backup of her identity, and then asks to retrieve her claim.

In order to retrieve her claim — which highlights how well she performed and confirms that her identity was indeed part of the network — Marta needs to perform a digital signature using her private key (more specifically, an EdDSA on Baby Jubjub).

For those of you less familiar with digital signatures, EdDSA stands for Edwards-curve Digital Signature Algorithm. Simply put, it’s a digital signature scheme that’s designed to be faster than existing schemes without sacrificing security.

With this claim in hand, Maria is now able to generate a zero-knowledge proof (zk-SNARK) from her smartphone browser.

This proof allows Marta to prove that she controls the private key of the identity linked to the claim she received from the application server. Remember that this claim is stored as a leaf inside a Merkle tree whose root is published on the Ethereum public blockchain.

The generation of the zk-proof in the smartphone browser is possible thanks to our websnark library. Websnark makes it possible to use #WASM in the browser to generate zero-knowledge proofs extremely fast (more specifically, a zk-SNARK proof using Groth16).

This zk-proof can then be sent (through a transaction-forwarder to avoid needing to directly pay gas) to the TrustCommunity smart contract. A transaction-forwarder is a server that forwards the transaction to the specified smart contract.

Once received, the TrustCommunity smart contract verifies the proof. And if everything checks out ok, airdrops the corresponding Nectar tokens to the user’s specified Ethereum address (as we’ll see later, this address is also contained inside the proof).

In sum, the end result of all this is that users are able to withdraw their Nectar tokens by sending a zk-proof to a smart contract, proving that they control an identity which has an assigned amount of Nectar, without revealing the specific identity in question.

As you may or may not know, algebraic circuits are a key part of zk-SNARKs. This is because zk-SNARKs cannot be applied to any computational problem directly; rather, you have to convert the problem into the right form.

And while we won’t dig into the details here, if you want to learn more about this conversion process we recommend you read through this excellent (three-part) post by Vitalik.

To facilitate the generation of zk-proofs, we’ve created a library called circom that allows you to build algebraic circuits to be used in zero knowledge proofs. More formally, it’s a circuit compiler for zk-SNARKs.

What do we mean exactly by a circuit? For our purposes, a circuit is equivalent to a statement or deterministic program which has an output and one or more inputs.

There are two types of possible inputs to a circuit: private and public. The difference being that a private input is hidden from the verifier.

The circuit associated with our TrustCommunity zk-SNARK is constructed using Circom and looks like this:

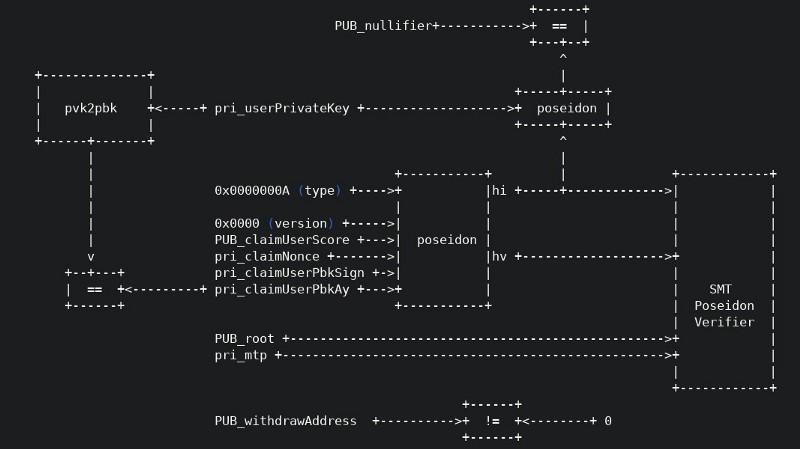
Circom is designed to work with websnark. In other words, any circuit you build in circom can be used in websnark.

We’ve also created a library called circomlib which contains some useful circuits already implemented in circom. For example, circomlib contains an implementation of the Poseidon hash function out of the box.

If you look closely at the image of the TrustCommunity circuit again you should be able to see that the circuit has four public inputs:

1. The amount of Nectar to withdraw (claimUserScore)
2. The recipient’s Ethereum withdrawal address (withdrawAddress)
3. The nullifier (a value deterministically calculated from other inputs, to avoid reusage of the zk-proofs)
4. The Merkle root of the valid Merkle tree (root)

As well as five private inputs. Importantly, the private inputs of the circuit include the private key of the user — a Baby JubJub private key (claimUserPbKay) and the Merkle proof of the claim (mtp).

And while exploring the details of circom is out of scope of this post, if you’re curious to learn more about how to use it to create circuits we recommend you got through our recently updated guide on the subject.

Even though it uses snarkjs — a JS implementation of the zk-SNARKs protocol — instead of websnark, it’s still useful: We cover the various techniques to write circuits, then move on to creating and verifying a zk-proof off-chain, and finish off by doing the same thing on-chain.

If you’ve made it this far, thank you for taking the time. We hope we’ve helped you demystify some of the magic and that you’ve come out with a deeper understanding of how it all works under the hood. Feel free to contact us on either twitter or telegram with any queries you may have! 💙