Sparse Merkle trees: a visual introduction
Posted by Sacha Saint-Leger on February 10, 2020
Building off our earlier post on Merkle trees, here we cover a slightly more complex data structure called a sparse Merkle tree. This is the data structure we use at Iden3.
A sparse Merkle tree is like a standard Merkle tree, except the contained data is indexed, and each data block is placed at the leaf that corresponds to that block’s index.
In addition to inheriting the tamper-resistance and proof-of-membership properties from normal Merkle trees, sparse Merkle trees make it easy to prove that some data doesn’t exist (proof of non-membership).
Proof of non-membership
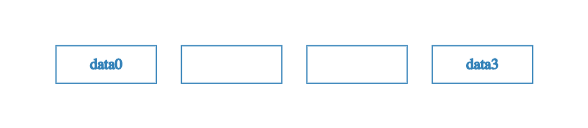
Say that this time we only have two pieces of data – data0 and data3 – with indices 0 and 3 respectively. To construct a sparse Merkle tree, we populate the 0th and 3rd leaves with this data, leaving the 1st and 2nd leaves empty.
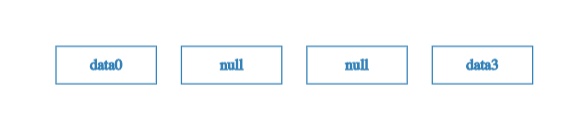
Well.. almost empty. To be precise, we fill the 1st and 2nd leaves in with a special placeholder value like null.
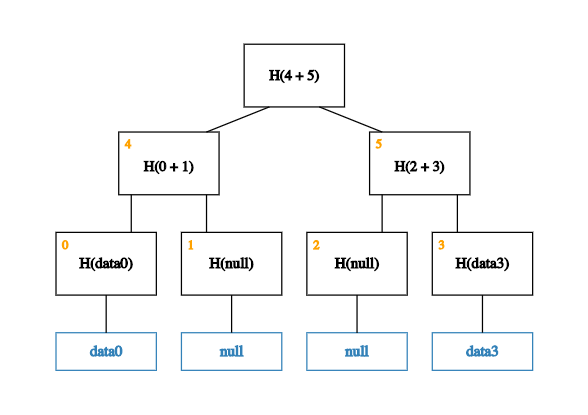
With this placeholder in place, we can now build up the rest of the tree.
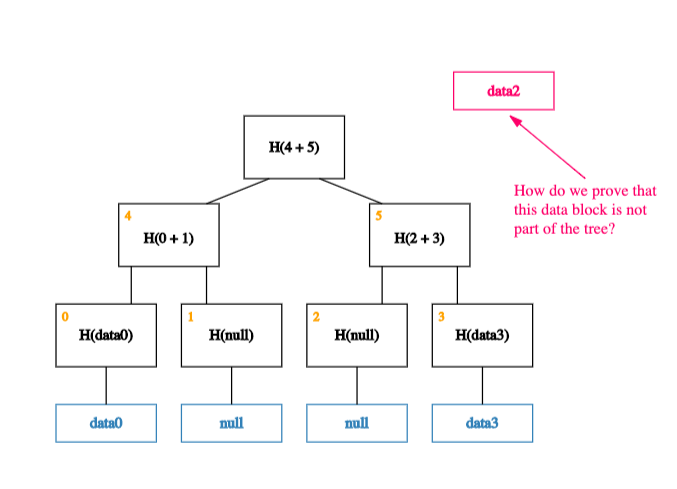
Now, what happens if we want to prove that a piece of (indexed) data – data2, say – is not a member of this tree?
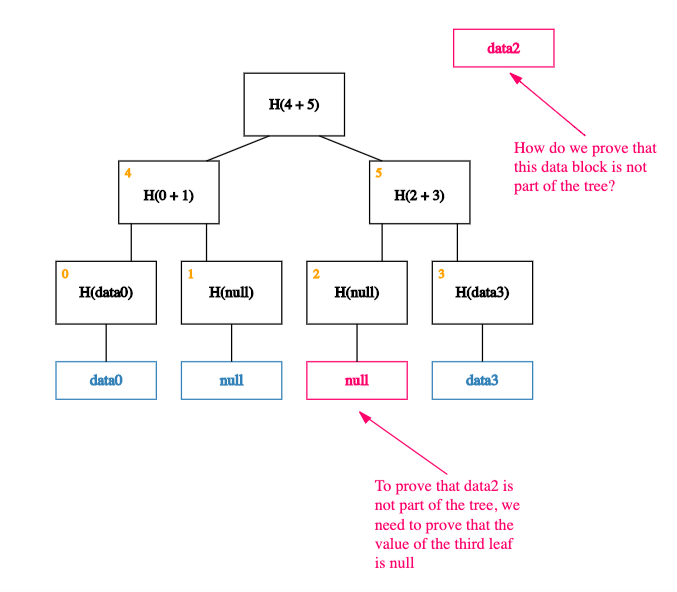
Thanks to the way our data is indexed, proving that data2 is not a member of the tree is equivalent to proving that the value of the leaf at index 2 is null!
Put another way, proving non-membership of a data block is equivalent to proving membership of null (a simple Merkle proof). And, as we saw in our previous post, doing this efficiently is a basic property of a Merkle tree.
Summary
In sum, by indexing data and leaving leaves empty, sparse Merkle trees allow us to reframe proofs of non-membership into proofs of membership (a.k.a Merkle proofs), making it easy to prove that some data does not exist.
One drawback to sparse Merkle trees is that they are really big. This means that, without optimizations, read and write operations can be quite inefficient.
For exampe: a sparse Merkle tree usually has 2^256 leaves vs 2^32 for a normal Merkle tree. This means naive implementations require 256 operations to read or write (vs 32).
Luckily, however, these sorts of inefficiencies are largely illusory. Since fairly simple optimizations exist to get around them!
Note: while we won’t get into the details here, one of the keys to these optimisations is that sparse Merkle trees are well, mostly sparse. This means many of the subtrees will end up being zero subtrees. Since H(0), H(H(0)), H(H(H(0))), and so on, are all constant values, the zero-subtrees can be cached (calculated once, stored, and then omitted from Merkle proofs), greatly reducing the size of computations.
Resources
Optimizing Sparse Merkle trees - Ethresearch post
Sparse Merkle trees - Iden3 paper
Our sparse Merkle tree implementations: